סיימת כיתה ג׳?׳

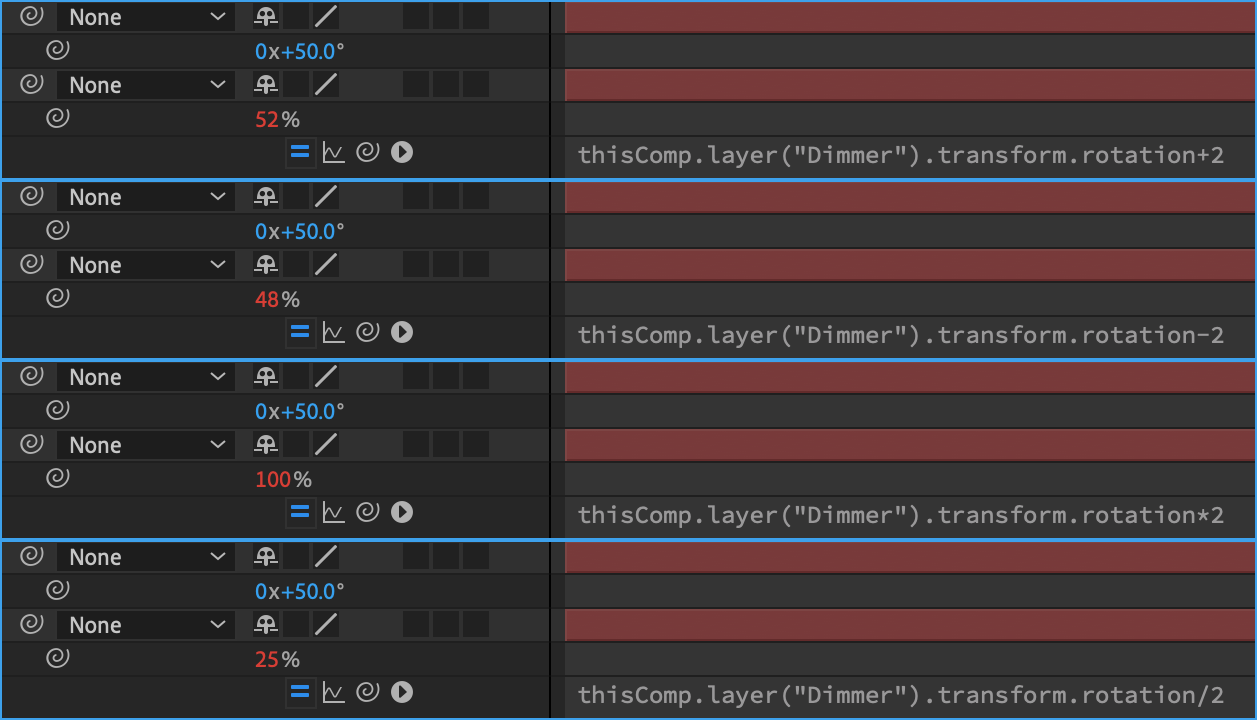
אם התשובה היא כן, סביר להניח שאתה מרגיש בנוח עם פעולות החשבון חיבור, חיסור, כפל וחילוק. כל אלה יכולים לסייע ביצירת החיבור המושלם בין מאפיינים, או לפחות להתקרב לשם. בגדול, אפשר להסתכל על ביטוי (אם שורת קוד אחת או עשר) כערך מספרי. ואם בערך מספרי עסיקנן, אז פעולות חשבוניות יכולות לקחת אותנו שלב אחד קדימה. איך? פשוט מבצעים פעולה חשבונית לצד הביטוי (ולא באמת משנה הצד… כמו בחשבון!). כפי שניתן לראות בדוגמא, מאפיין האטימות לוקח את ערך הסיבוב של שכבה אחרת ותוספת של פעולה חשבונית משנה את הערך המתקבל על ערך האטימות :

ערך מקור: 50

חיבור: 52

חיסור: 48

כפל: 100

חילוק: 25

דוגמאות ושימושים:

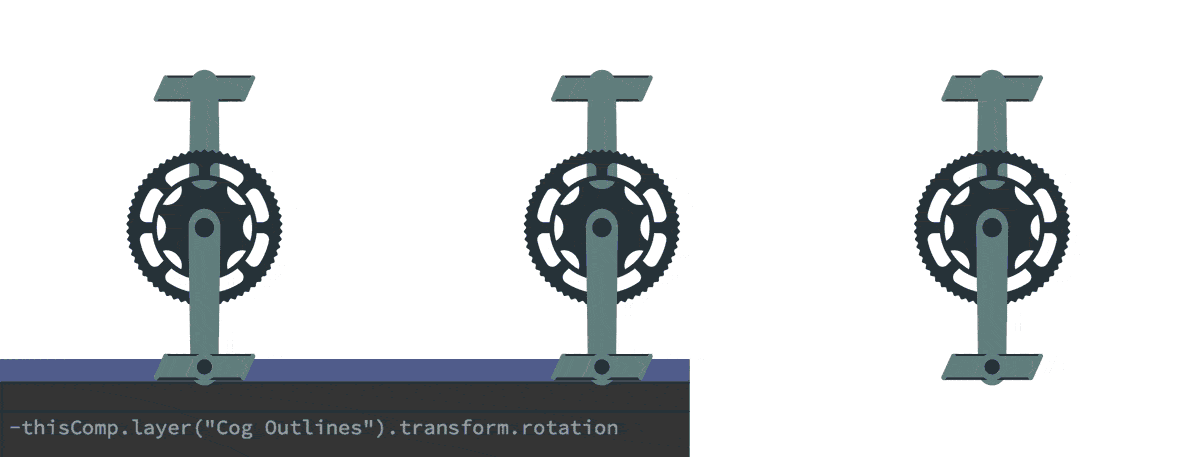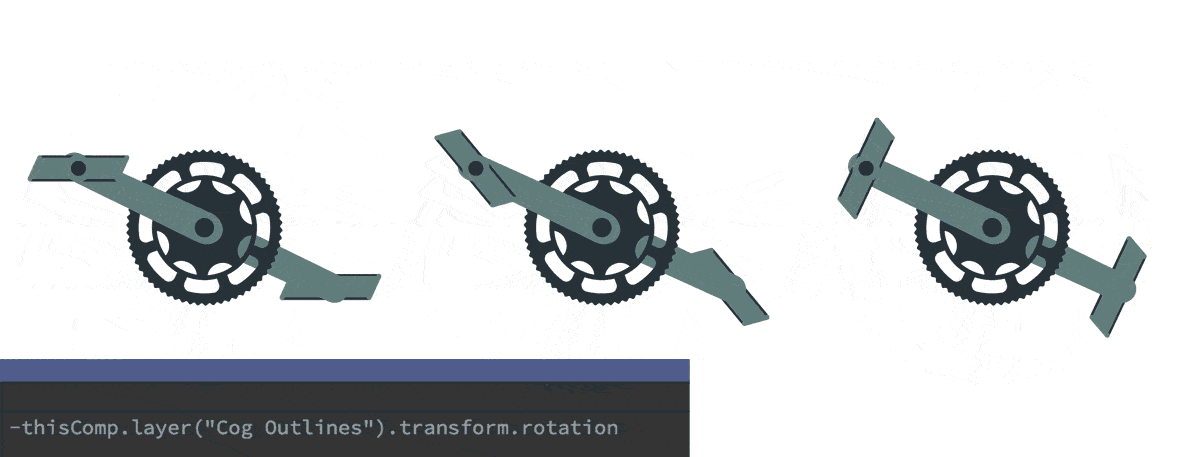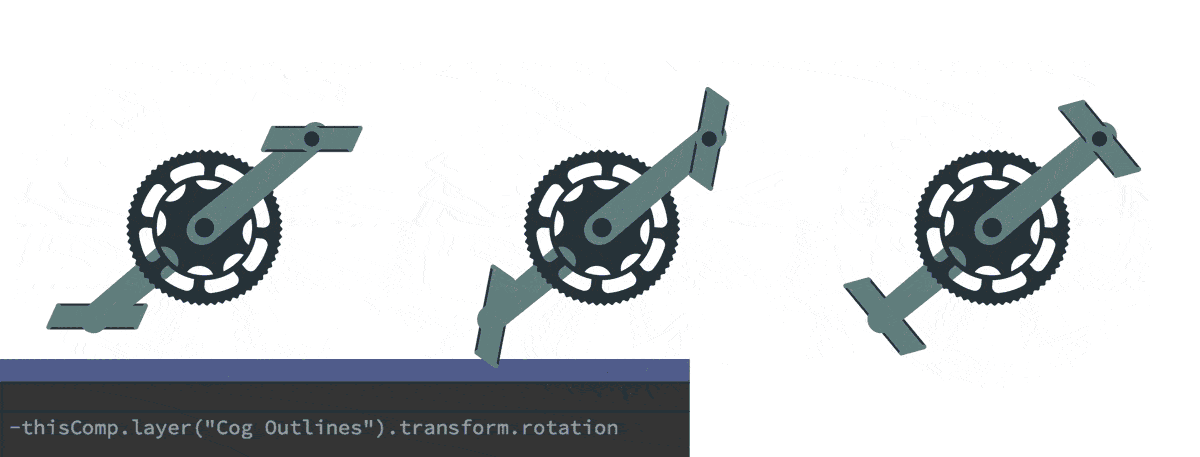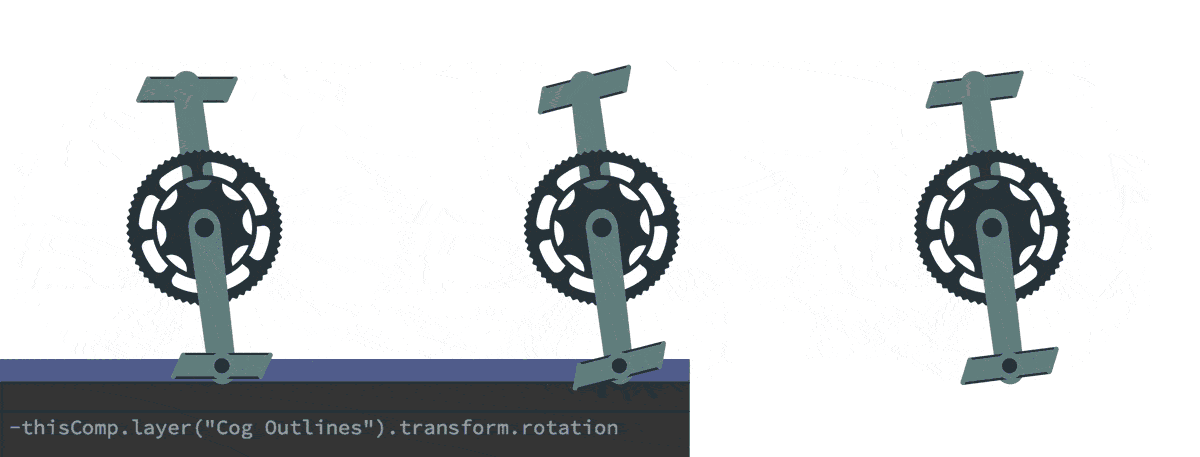
היפוך כיוון – אופניים 

היפוך כיוון הוא דבר מאוד נפוץ, אותו ניתן ליישם בחיבורים בהם יש צורך להפוך את ״כיוון״ החיבור, או להפוך ערכים חיוביים לשליליים וההיפך. בדוגמא זאת ניתן לראות שתי דוושות המחוברות בהורות רגילה לגלגל הינע. מצד ימין ניתן לראות כי הסיבוב של גלגל ההינע משנה את זווית הדוושות. במרכז ניתן לראות שכאשר מוסיפים חיבור מאפיין בין מאפייני הסיבוב, בנוסף להורות, מתקבל סיבוב עצמי של הדוושות על פי זווית האב. בדוגמא הימנית ניתן לראות כי הוספת מינוס (-) לפני הביטוי מתקבל סיבוב הופכי לסיבוב האב, כך שהדוושות שומרות על זווית ישרה.

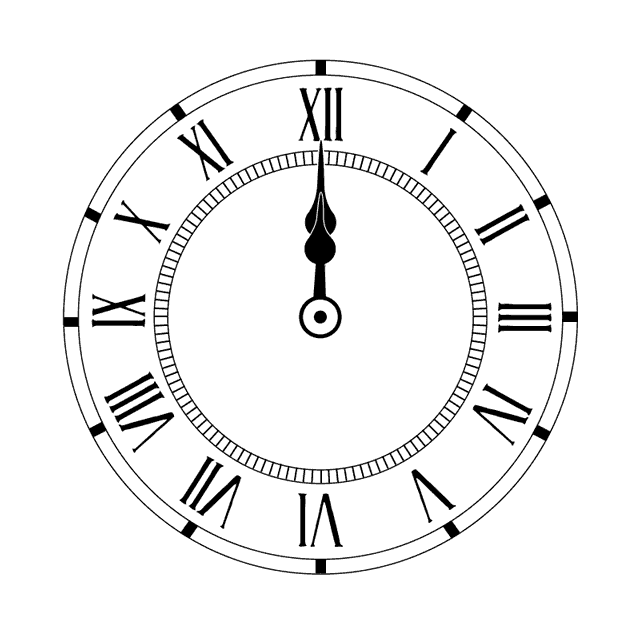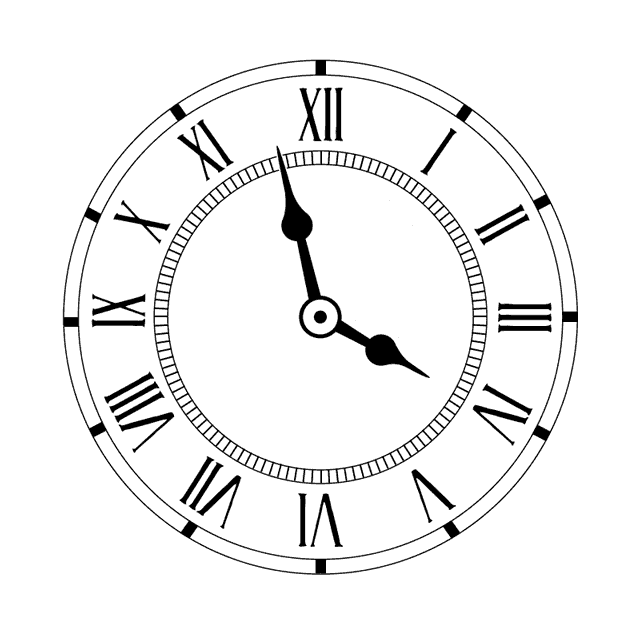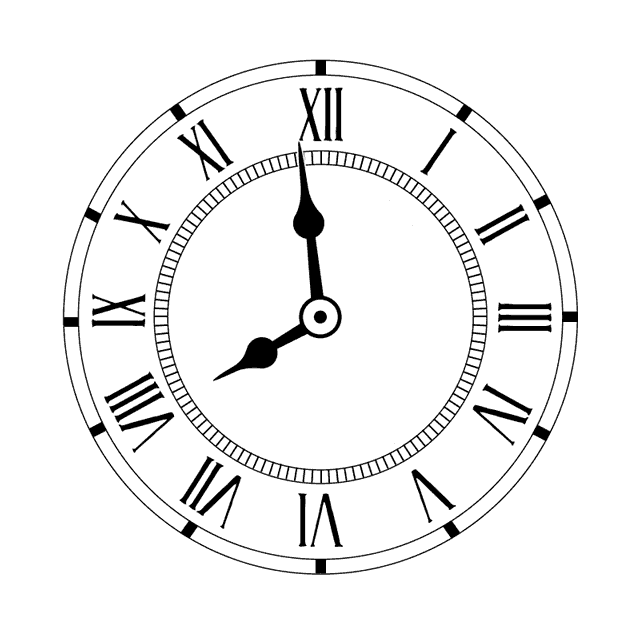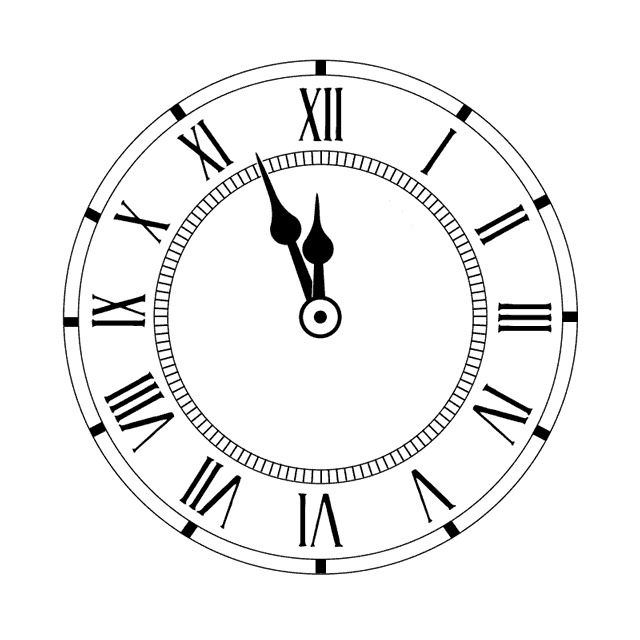
ריג שעון

יצירת היחס המתאים בין שתי שכבות יכולה לייצר מערכת העובדת באותה מכניקה בה היא עובדת בעולם האמיתי. בדוגמא זו ניתן לראות חיבור בין מחוג השעות למחוג הדקות בשעון אנאלוגי. מחוג השעות לוקח את ערך הסיבוב של מחוג הדקות באמצעות חיבור מאפיינים, אך ערך זה מחולק ב-12, מה שגורם למחוג השעות לעשות סיבוב שלם רק לאחר 12 סיבובים של מחוג הדקות, כפי שקורה בשעון אמיתי. 

ריג גלגלי שיניים

נכון, אפשר להחליף כל סוג של ביטוי באמצעות קיפריימים, אבל בדוגמא זו המרחק, מבחינת בזבוז זמן, הוא קיצוני. הנפשה של גלגלי שיניים חייבת להיות מסונכרנת לכל אורכה ובצורה המדויקת ביותר. בכל נסיון להנפיש (מבלי להכנס לחישובים) האנימציה תצא בסופו של דבר מסנכרון, דבר שיגרור הרבה סבבי תיקונים ועריכה לאנימציה. הבנה שהיחס בין כמויות גלגלי השיניים הוא המפתח לפיצוח הביטוי הרצוי יגרום לאנימציה לעבוד בסנכרון באופן קבוע ובצורה אוטומטית. בדוגמא ניתן לראות כי מכפלה של הביטוי ביחס (חלוקה) שנוצרה בין כמות השיניים בכל גלגל תייצר אנימציה מסונכרנת בצורה הזריזה ביותר.

רוב הדוגמאות במאמר זה נעשו על ערך הסיבוב של השכבה, אך ניתן להשתמש במידע זה לחיבור בין כל המאפיינים, כל עוד מדובר במאפיין בעל ערך בודד. לאפטר אפקטס לא ״אכפת״ אם הערך הוא באחוזים, מעלות, פיקסלים או יחידות זמן. בסופו של דבר מה שחשוב הוא שמדובר בערך מספרי, ולייצר עבורו את המניפולציה המתאימה לצורכי האנימציה שלנו. 

ניתן להוריד את קובץ הפרויקט מקישור זה arithmetic.aep לשחק עם הערכים וליצור חיבורים חדשים. בהצלחה!

למאמר הקודם